10 Inverse Laplace Transform

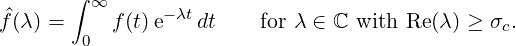
For a real valued function f such that t⟼f(t)e-σ_ct is integrable over ℝ⁺, we can define its Laplace transform

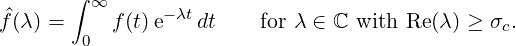To use the following functions, you should include pnl/pnl_laplace.h.

typedef struct 
{ 
  dcomplex (*F) (dcomplex x, void *params); 
  void *params; 
} PnlCmplxFunc;

• double pnl_ilap_euler (PnlCmplxFunc *fhat, double t, int N, int M)
  Description Compute f(t) where f is given by its Laplace transform fhat by numerically inverting the Laplace transform using Euler’s summation. The values N = M = 15 usually give a very good accuracy. For more details on the accuracy of the method.

• double pnl_ilap_cdf_euler (PnlCmplxFunc *fhat, double t, double h, int N, int M)
  Description Compute the cumulative distribution function F(t) where F(x) = ∫ ₀^xf(t)dt and f is a density function with values on the positive real linegiven by its Laplace transform fhat. The computation is carried out by numerical inversion of the Laplace transform using Euler’s summation. The values N = M = 15 usually give a very good accuracy. The parameter h is the discretization step, the algorithm is very sensitive to the choice of h.

• double pnl_ilap_fft (PnlVect *res, PnlCmplxFunc *fhat, double T, double eps)
  Description Compute f(t) for t ∈ [h,T] on a regular grid and stores the values in res, where h = T∕size(res). The function f is defined by its Laplace transform fhat, which is numerically inverted using a Fast Fourier Transform algorithm. The size of res is related to the choice of the relative precision eps required on the value of f(t) for all t ≤T.

• double pnl_ilap_gs (PnlFunc *fhat, double t, int n)
  Description Compute f(t) where f is given by its Laplace transform fhat by numerically inverting the Laplace transform using a weighted combination of different Gaver Stehfest’s algorithms. Note that this function does not need the complex valued Laplace transform but only the real valued one. n is the number of terms used in the weighted combination.

• double pnl_ilap_gs_basic (PnlFunc *fhat, double t, int n)
  Description Compute f(t) where f is given by its Laplace transform fhat by numerically inverting the Laplace transform using Gaver Stehfest’s method. Note that this function does not need the complex valued Laplace transform but only the real valued one. n is the number of iterations of the algorithm. Note :  This function is provided for test purposes only. The function pnl_ilap_gs gives far more accurate results.