11 Ordinary differential equations

11.1 Overview

To use these functionalities, you should include pnl/pnl_integration.h.

These functions are designed for numerically solving n-dimensional first order ordinary differential equation of the general form

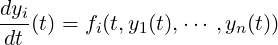The system of equations is defined by the following structure

typedef struct 
{ 
  void (*F) (int neqn, double t, const double *y, double *yp, void *params); 
  int neqn; 
  void *params; 
} PnlODEFunc ;

• int neqn
  Description Number of equations

• void * params
  Description An untyped structure used to pass extra arguments to the function f defining the system

• void (* F) (int neqn, double t, const double *y, double *yp, void *params)
  Description After calling the fuction, yp should be defined as follows yp_i = f_i(neqn, t, y, params). y and yp should be both of size neqn

We provide the following macro to evaluate a PnlODEFunc at a given point

#define PNL_EVAL_ODEFUNC(Fstruct, t, y, yp) \ 
    (*((Fstruct)->F))((Fstruct)->neqn, t, y, yp, (Fstruct)->params)

11.2 Functions

• int pnl_ode_rkf45 (PnlODEFunc *f, double *y, double t, double t_out, double relerr, double abserr, int *flag)
  Description This function computes the solution of the system defined by the PnlODEFunc f at the point t_out. On input, (t,y) should be the initial condition, abserr,relerr are the maximum absolute and relative errors for local error tests (at each step, abs(local error) should be less that relerr * abs(y) + abserr). Note that if abserr = 0 or relerr = 0 on input, an optimal value for these variables is computed inside the function The function returns an error OK or FAIL. In case of an OK code, the y contains the solution computed at t_out, in case of a FAIL code, flag should be examined to determine the reason of the error. Here are the different possible values for flag

  • flag = 2 : integration reached t_out, it indicates successful return and is the normal mode for continuing integration.

  • flag = 3 : integration was not completed because relative error tolerance was too small. relerr has been increased appropriately for continuing.

  • flag = 4 : integration was not completed because more than 3000 derivative evaluations were needed. this is approximately 500 steps.

  • flag = 5 : integration was not completed because solution vanished making a pure relative error test impossible. must use non-zero abserr to continue. using the one-step integration mode for one step is a good way to proceed.

  • flag = 6 : integration was not completed because requested accuracy could not be achieved using smallest allowable stepsize. user must increase the error tolerance before continued integration can be attempted.

  • flag = 7 : it is likely that rkf45 is inefficient for solving this problem. too much output is restricting the natural stepsize choice. use the one-step integrator mode. see pnl_ode_rkf45_step.

  • flag = 8 : invalid input parameters this indicator occurs if any of the following is satisfied - neqn <= 0, t=tout, relerr or abserr <= 0.

• int pnl_ode_rkf45_step (PnlODEFunc *f, double *y, double *t, double t_out, double *relerr, double abserr, double *work, int *iwork, int *flag)
  Description Same as pnl_ode_rkf45 but it only computes one step of integration in the direction of t_out. work and iwork are working arrays of size 3 + 6 * neqn and 5 respectively and should remain untouched between successive calls to the function. On output t holds the point at which integration stopped and y the value of the solution at that point.