Fast Fourier Transform

9 Fast Fourier Transform

9.1 Overview

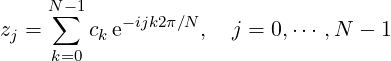
This toolbox uses C version of the Fortran FFTPack library available on http://www.netlib.org/fftpack.

The forward Fourier transform of a vector c is defined by

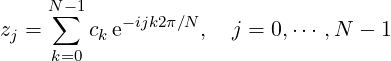N∑- 1 -ijk2π∕N zj = cke , j = 0,⋅⋅⋅ ,N - 1 k=0

The inverse Fourier transform enables to recover c from z and is defined by

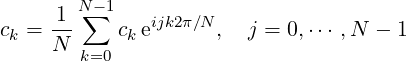N∑- 1 ck = -1 ckeijk2π∕N, j = 0,⋅⋅⋅ ,N - 1 N k=0

Note that the inverse Fourier transform is scaled by 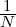, such that the inverse Fourier transform applies to the Fourier transform just yields the original vector.

The coefficients of the Fourier transform of a real function satisfy the following relation

zk = zN-k,

(3)

where N is the number of discretization points.

A few remarks on the FFT of real functions and its inverse transform:

We only need half of the coefficients.
When a value is known to be real, its imaginary part is not stored. So the imaginary part of the zero-frequency component is never stored as it is known to be zero.
For a sequence of even length the imaginary part of the frequency n∕2 is not stored either, since the symmetry (3) implies that this is purely real too.

FFTPack storage The functions use the fftpack storage convention for half-complex sequences. In this convention, the half-complex transform of a real sequence is stored with frequencies in increasing order, starting from zero, with the real and imaginary parts of each frequency in neighboring locations.

The storage scheme is best shown by some examples. The table below shows the output for an odd-length sequence, n = 5. The two columns give the correspondence between the 5 values in the half-complex sequence (stored in a PnlVect V ) and the values (PnlVectComplex C) that would be returned if the same real input sequence were passed to pnl_fft as a complex sequence (with imaginary parts set to 0),

C(0) = V(0) + i0, C(1) = V(1) + iV (2), C(2) = V(3) + iV (4), ----- C(3) = V(3) - iV (4) = C-(2), C(4) = V(1) + iV (2) = C (1)

(4)

The elements of index greater than N∕2 of the complex array, as C(3) and C(4) are filled in using the symmetry condition.

The next table shows the output for an even-length sequence, n = 6. In the even case, there are two values which are purely real,

C(0) = V(0) + i0, C(1) = V(1) + iV (2), C(2) = V(3) + iV (4),--- C(3) = V(5) - i0 = C (0),--- C(4) = V(3) - iV (4) = C-(2), C(5) = V(1) + iV (2) = C (1)

(5)

9.2 Functions

To use the following functions, you should include pnl/pnl_fft.h.

9.2.1 Direct call functions

All FFT functions need some extra memory to perform their computations. This is automatically handled by all the functions but you can these repeatedly, for instance inside a Monte Carlo loop, you should allocate a workspace once and for all and use the same at every iteration. In this case, use the functions defined in Section 9.2.2.

int pnl_fft_inplace (PnlVectComplex *data)
Description Compute the FFT of data in place. The original content of data is lost.
int pnl_ifft_inplace (PnlVectComplex *data)
Description Compute the inverse FFT of data in place. The original content of data is lost.
int pnl_fft (const PnlVectComplex *in, PnlVectComplex *out)
Description Compute the FFT of in and stores it into out.
int pnl_ifft (const PnlVectComplex *in, PnlVectComplex *out)
Description Compute the inverse FFT of in and stores it into out.
int pnl_fft2 (double *re, double *im, int n)
Description Compute the FFT of the vector of length n whose real (resp. imaginary) parts are given by the arrays re (resp. im). The real and imaginary parts of the FFT are respectively stored in re and im on output.
int pnl_ifft2 (double *re, double *im, int n)
Description Compute the inverse FFT of the vector of length n whose real (resp. imaginary) parts are given by the arrays re (resp. im). The real and imaginary parts of the inverse FFT are respectively stored in re and im on output.
int pnl_real_fft (const PnlVect *in, PnlVectComplex *out)
Description Compute the FFT of the real valued sequence in and stores it into out.
int pnl_real_ifft (const PnlVectComplex *in, PnlVect *out)
Description Compute the inverse FFT of in and stores it into out. The vector in is supposed to be the FFT of a real valued vector.
int pnl_real_fft_inplace (double *data, int n)
Description Compute the FFT of the real valued vector data of length n. The result is stored in data using the FFTPack storage described above, see 9.1.0.0.
int pnl_real_ifft_inplace (double *data, int n)
Description Compute the inverse FFT of the vector data of length n. data is supposed to be the FFT coefficients a real valued sequence stored using the FFTPack storage. On output, data contains the inverse FFT.
int pnl_real_fft2 (double *re, double *im, int n)
Description Compute the FFT of the real vector re of length n. im is only used on output to store the imaginary part the FFT. The real part is stored into re
int pnl_real_ifft2 (double *re, double *im, int n)
Description Compute the inverse FFT of the vector re + i * im of length n, which is supposed to be the FFT of a real valued sequence. On exit, im is unused.
int pnl_fft2d_inplace (PnlMatComplex *data)
Description Compute the 2D FFT of data. This function applies a 1D FFT to each row of the matrix and then a 1D FFT to each column of the modified matrix.
int pnl_ifft2d_inplace (PnlMatComplex *data)
Description Compute the inverse 2D FFT of data. This function is the inverse of the function pnl_fft2d_inplace.
int pnl_fft2d (const PnlMatComplex *in, PnlMatComplex *out)
Description Compute the 2D FFT of in and stores it into out.
int pnl_ifft2d (const PnlMatComplex *in, PnlMatComplex *out)
Description Compute the inverse 2D FFT of in and stores it into out.
int pnl_real_fft2d (const PnlMat *in, PnlMatComplex *out)
Description Compute the 2D FFT of the real matrix in and stores it into out.
int pnl_real_ifft2d (const PnlMatComplex *in, PnlMatComplex *out)
Description Compute the inverse 2D FFT of the complex matrix in which is known to be the forward 2D FFT a real matrix. The result id stored it into out. Note that this function modifies the input matrix in.

9.2.2 Function with workspace

double* pnl_fft_alloc_wspace (const char *func, int n)
Description Return an allocated workspace array ready yo use for function func and input data of size n
int pnl_fft_inplace_with_wspace (PnlVectComplex *data, double *wspace)
Description Compute the FFT of data in place. The original content of data is lost.
int pnl_ifft_inplace_with_wspace (PnlVectComplex *data, double *wspace)
Description Compute the inverse FFT of data in place. The original content of data is lost.
int pnl_real_fft_inplace_with_wspace (double *data, double *wspace, int n)
Description Compute the inverse FFT of in and stores it into out. The vector in is supposed to be the FFT of a real valued vector.
int pnl_real_ifft_inplace_with_wspace (double *data, double *wspace, int n)
Description Compute the inverse FFT of the vector data of length n. data is supposed to be the FFT coefficients a real valued sequence stored using the FFTPack storage. On output, data contains the inverse FFT.
int pnl_real_fft_with_wspace (const PnlVect *in, PnlVectComplex *out, double *wspace)
Description Compute the FFT of the real valued sequence in and stores it into out.
int pnl_real_ifft_with_wspace (const PnlVectComplex *in, PnlVect *out, double *wspace)
Description Compute the inverse FFT of in and stores it into out. The vector in is supposed to be the FFT of a real valued vector.

[next] [prev] [prev-tail] [front] [up]