Function bases and regression

7 Function bases and regression

7.1 Overview

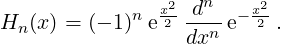
To use these functionalities, you should include pnl/pnl_basis.h.

struct _PnlBasis 
{ 
  /** 
    * Must be the first element in order for the object mechanism to work 
    * properly. This allows any PnlBasis pointer to be cast to a PnlObject 
    */ 
  PnlObject     object; 
  /** The basis type */ 
  int           id; 
  /** The string to label the basis */ 
  const char   *label; 
  /** The number of variates */ 
  int           nb_variates; 
  /** The total number of elements in the basis */ 
  int           nb_func; 
  /** The sparse Tensor matrix */ 
  PnlSpMatInt  *SpT; 
  /** The number of functions in the tensor @p SpT */ 
  int           len_T; 
  /** Compute the i-th element of the one dimensional basis.  As a convention, (*f)(x, 0) MUST be equal to 1 */ 
  double      (*f)(double x, int i, int dim, void *params); 
  /** Compute the first derivative of i-th element of the one dimensional basis */ 
  double      (*Df)(double x, int i, int dim, void *params); 
  /** Compute the second derivative of the i-th element of the one dimensional basis */ 
  double      (*D2f)(double x, int i, int dim, void *params); 
  /** PNL_TRUE if the basis is reduced */ 
  int           isreduced; 
  /** The center of the domain */ 
  double       *center; 
  /** The inverse of the scaling factor to map the domain to [-1, 1]^nb_variates */ 
  double       *scale; 
  /** An array of additional functions */ 
  PnlRnFuncR   *func_list; 
  /** The number of functions in @p func_list */ 
  int           len_func_list; 
  /** Extra parameters to pass to basis functions */ 
  void         *f_params; 
  /** Size of params in bytes to be passed to malloc */ 
  size_t        f_params_size; 
  /** Non linear mapping of the data */ 
  double       (*map)(double x, int dim, void *params); 
  /** First derivative of the non linear mapping  */ 
  double       (*Dmap)(double x, int dim, void *params); 
  /** Second derivate of the linear mapping */ 
  double       (*D2map)(double x, int dim, void *params); 
  /** Extra parameters for map, Dmap and D2map */ 
  void          *map_params; 
  /** Size of @p map_params in bytes to be passed to malloc */ 
  size_t         map_params_size; 
};

A PnlBasis is a family of multivariate functions with real values. Two different kinds of functions can be stored in these families: tensor functions — originally, this was the only possibility — and standard multivariate function typed as PnlRnFuncR.

7.1.1 Tensor functions

Tensor functions are built as a tensor product of one dimensional elements. Hence, we only need a tensor matrix T to describe a multi-dimensional basis in terms of the one dimensional one. These tensors functions can be easily evaluated and differentiated twice, see pnl_basis_eval, pnl_basis_eval_vect, pnl_basis_eval_D, pnl_basis_eval_D_vect, pnl_basis_eval_D2, pnl_basis_eval_D2_vect, pnl_basis_eval_derivs, pnl_basis_eval_derivs_vect.

Three bases are already registered as listed in Table 3. A new tensor basis can be registered using the function pnl_basis_type_register.

PNL_BASIS_CANONICAL		for the Canonical polynomials
PNL_BASIS_HERMITE		for the Hermite polynomials
PNL_BASIS_TCHEBYCHEV		for the Tchebychev polynomials

Table 3: Names of the bases.

The Hermite polynomials are defined by

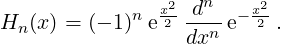H (x) = (- 1)n ex22-dn-e- x22-. n dxn

If G is a real valued standard normal random variable, E[H_n(G)H_m(G)] = n!1.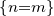

The two tensors T and SpT do actually store the same information — T(i,j) is the degree w.r.t the j-th variable in the i-th function. Originally, we were only using the dense representation T, which is far more convenient to use when building the basis but it slows down the evaluation of the basis by a great deal. To overcome this lack of efficiency, a sparse storage was added. Such a basis can be created using one of the following functions.

PnlBasis * pnl_basis_create (int index, int nb_func, int nb_variates)
Description Create a PnlBasis for the family defined by index (see Table 3 and pnl_basis_type_register) with nb_variates variates. The basis will contain nb_func.
PnlBasis * pnl_basis_create_from_degree (int index, int degree, int nb_variates)
Description Create a PnlBasis for the family defined by index (see Table 3 and pnl_basis_type_register) with total degree less or equal than degree and nb_variates variates. The total degree is the sum of the partial degrees.
PnlBasis * pnl_basis_create_from_prod_degree (int index, int degree, int nb_variates)
Description Create a PnlBasis for the family defined by index (see Table 3 and pnl_basis_type_register) with total degree less or equal than degree and nb_variates variates. The total degree is the product of MAX(1, d_i) where the d_i are the partial degrees.
PnlBasis * pnl_basis_create_from_hyperbolic_degree (int index, double degree, double q, int n)
Description Create a sparse basis of polynomial with n variates. We give the example of the Canonical basis. A canonical polynomial with n variates writes X₁^α₁X₂^α₂…X_n^α_n. To be a member of the basis, it must satisfy 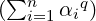^1∕q ≤degree. This kind of basis based on an hyperbolic set of indices gives priority to polynomials associated to low order interaction.
PnlBasis * pnl_basis_create_from_tensor (int index, PnlMatInt *T)
Description Create a PnlBasis for the polynomial family defined by index (see Table 3) using the basis described by the tensor matrix T. The number of lines of T is the number of functions of the basis whereas the numbers of columns of T is the number of variates of the functions.
Here is an example of a tensor matrix. Assume you are working with three variate functions, the basis { 1, x, y, z, x^2, xy, yz, z^3} is decomposed in the one dimensional canonical basis using the following tensor matrix
$( ) 0 0 0 || 1 0 0 || || 0 1 0 || || || || 0 0 1 || || 2 0 0 || || 1 1 0 || ( 0 1 1 ) 0 0 3$
PnlBasis * pnl_basis_create_from_sparse_tensor (int index, PnlSpMatInt *SpT)
Description Create a PnlBasis for the polynomial family defined by index (see Table 3) using the basis described by the sparse tensor matrix SpT. The number of lines of SpT is the number of functions of the basis whereas the numbers of columns of SpT is the number of variates of the functions.
void pnl_basis_set_from_tensor (PnlBasis *b, int index, const PnlMatInt *T)
Description Set an alredy existing basis b to a polynomial family defined by index (see Table 3) using the basis described by the tensor matrix T. The number of lines of T is the number of functions of the basis whereas the numbers of columns of T is the number of variates of the functions.
Same function as pnl_basis_create_from_tensor except that it operates on an already existing basis.

7.1.2 Local basis functions

A local basis is a family of indicator functions of a Cartesian partition of [-1,1]^d. Let (n_i)_{i∈{1,…,d}} be the number of interval along each direction. An element of the partition write

d∏ [ ] Ak = - 1 + ki,- 1+ ki-+-1 i=1 ni ni

where k is the multi-index defined by k_i ∈{0,…,n_i - 1} for all i ∈{1,…,d}. These functions are orthogonal for the standard L² scalar product; this property is used by pnl_basis_fit_ls. Note that they are not differentiable.

We provide the helper function pnl_basis_local_get_index to compute the linear representation of the multi-index k.

PnlBasis * pnl_basis_local_create (int *n_intervals, int space_dim)
Description Create a local basis with n_intervals[i - 1] intervals along dimension i for all i ∈{1,…,space_dim}
PnlBasis * pnl_basis_local_create_regular (int n_intervals, int space_dim)
Description Equivalent to calling pnl_basis_local_create with an array of size space_dim filled with n_intervals.
int pnl_basis_local_get_index (const PnlBasis *basis, const double *x)
Description Return the linear index of the cell containing x. It is an integer between 0 and (∏ _i=1^dn_i) - 1.

If the domain you want to consider is not [-1,1]^d, use the functions pnl_basis_set_domain, pnl_basis_set_reduced and pnl_basis_set_map to map your product space into [-1,1]^d.

7.1.3 Standard multivariate functions

These functions are supposed to be PnlRnFuncR.

To make this toolbox more complete, it is now possible to add some extra functions, which are not tensor product. They are stored using an independent mechanism in func_list. These additional functions are only taken into account by the methods pnl_basis_i, pnl_basis_i_vect, pnl_basis_eval and pnl_basis_eval_vect. Note in particular that it is not possible to differentiate these functions and that they are not sensitive to the isreduced attribute. To add an extra function to an existing PnlBasis, call the function

void pnl_basis_add_function (PnlBasis *b, PnlRnFuncR *f)
Description Add the function f to the already existing basis b.

7.2 Functions

PnlBasis * pnl_basis_new ()
Description Create an empty PnlBasis .
void pnl_basis_clone (PnlBasis *dest, const PnlBasis *src)
Description Clone src into dest. The basis dest must already exist before calling this function. On exit, dest and src are identical and independent.
PnlBasis * pnl_basis_copy (const PnlBasis *B)
Description Create a copy of B.
void pnl_basis_free (PnlBasis **basis)
Description Free a PnlBasis created by pnl_basis_create. Beware that basis is the address of a PnlBasis *.
void pnl_basis_del_elt (PnlBasis *B, const PnlVectInt *d)
Description Remove the function defined by the tensor product d from an existing basis B.
void pnl_basis_del_elt_i (PnlBasis *B, int i)
Description Remove the i-th element of basis B.
void pnl_basis_add_elt (PnlBasis *B, const PnlVectInt *d)
Description Add the function defined by the tensor d to the Basis B.
int pnl_basis_type_register (const char *name, double (*f)(double, int, int, void), double (*Df)(double, int, int, void), double (*D2f)(double, int, int, void), int is_orthogonal)
Description Register a new basis type and return the index to be passed to pnl_basis_create. The variable name is a unique string identifier of the family. The variables f, Df, D2f are the one dimensional basis functions, its first and second order derivatives. Each of these functions must return a double and take two arguments : the first one is the point at which evaluating the basis functions, the second one is the index of function. The varis_orthogonal if the elements of the basis are orthogonal for the L² scalar product. Here is a toy example to show how the canonical basis is registered (this family is actually already available with the id PNL_BASIS_CANONICAL, so the following example may look a little fake)
```
  double f(double x, int n, int dim, void *params) { return pnl_pow_i(x, n); } 
  double Df(double x, int n, int dim, void *params) { return n * pnl_pow_i(x, n-1); } 
  double f(double x, int n, int dim, void *params) { return n * (n-1) * pnl_pow_i(x, n-2); } 
 
  int id = pnl_basis_register ("Canonic", f, Df, D2f, PNL_FALSE); 
  /* 
   * B is the Canonical basis of polynomials with degree less or equal than 2 in dimension 5. 
   */ 
  PnlBasis *B = pnl_basis_create_from_degree (id, 2, 5);
```
void pnl_basis_print (const PnlBasis *B)
Description Print the characteristics of a basis.

Functional regression based on a least square approach often leads to ill conditioned linear systems. One way of improving the stability of the system is to use centered and renormalized polynomials so that the original domain of interest D (a subset of ℝ^d) is mapped to [-1,1]^d. If the domain D is rectangular and writes [a,b] where a,b ∈ ℝ^d, the reduction mapping is done by

( xi --(bi +-ai)∕2) x ∈ D ↦- → (bi - ai)∕2 i=1,⋅⋅⋅,d

(1)

void pnl_basis_set_domain (PnlBasis *B, const PnlVect *a, const PnlVect *b)
Description This function declares B as a centered and normalized basis as defined by Equation 1. Calling this function is equivalent to calling pnl_basis_set_reduced with center=(b+a)/2 and scale=(b-a)/2.
void pnl_basis_set_reduced (PnlBasis *B, const PnlVect *center, const PnlVect *scale)
Description This function declares B as a centered and normalized basis using the mapping

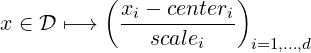$( ) xi --centeri x ∈ D ↦-→ scalei i=1,...,d$
void pnl_basis_reset_reduced (PnlBasis *B)
Description Reset the reduction settings.

Note that this renormalization does not apply to the extra functions by pnl_basis_add_function but only to the functions defined by the tensor T.

It is also possible to apply a non linear map φ_i : ℝ →ℝ to the i-th coordinate of the input variable before the reduction operation if any. Then, the input variables are transformed according to

( ) x ∈ D ↦-→ φi(xi)--(bi +-ai)∕2 (bi - ai)∕2 i=1,...,d

(2)

void pnl_basis_set_map (PnlBasis *B, double (*map)(double x, int i, void*params), double (*Dmap)(double x, int i, void*params), double (*D2map)(double x, int i, void*params), void *params, size_t size_params)
Description Define the non linear applied to the input variables before the reduction operation. The parameters Dmap and D2map can be NULL. The three functions map, Dmap and D2map take as second argument the index of the coordinate, while their third argument is used to passe extra parameters defined by params.

int pnl_basis_fit_ls (PnlBasis *P, PnlVect *coef, PnlMat *x, PnlVect *y)
Description Compute the coefficients coef defined by

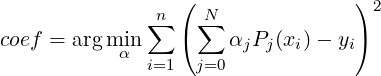$∑n ( N∑ )2 coef = arg min ( αjPj(xi)- yi) α i=1 j=0$

where N is the number of functions to regress upon and n is the number of points at which the values of the original function are known. P_j is the j -th basis function. Each row of the matrix x defines the coordinates of one point x_i. The function to be approximated is defined by the vector y of the values of the function at the points x.
double pnl_basis_ik_vect (const PnlBasis *b, const PnlVect *x, int i, int k)
Description An element of a basis writes ∏ _l=0^nb_variatesϕ_l(x_l) where the ϕ’s are one dimensional polynomials. This functions computes the therm ϕ_k of the i-th basis function at the point x.
double pnl_basis_i_vect (const PnlBasis *b, const PnlVect *x, int i)
Description If b is composed of f₀,…,f_{nb_func-1}, then this function returns f_i(x).
double pnl_basis_i_D_vect (const PnlBasis *b, const PnlVect *x, int i, int j)
Description If b is composed of f₀,…,f_{nb_func-1}, then this function returns ∂_{x_j}f_i(x).
double pnl_basis_i_D2_vect (const PnlBasis *b, const PnlVect *x, int i, int j1, int j2)
Description If b is composed of f₀,…,f_{nb_func-1}, then this function returns ∂²_{x_j1,x_j2}f_i(x).
void pnl_basis_eval_derivs_vect (const PnlBasis *b, const PnlVect *coef, const PnlVect *x, double *fx, PnlVect *Dfx, PnlMat *D2fx)
Description Compute the function, the gradient and the Hessian matrix of ∑ _k=0ⁿcoef_kP_k(⋅) at the point x. On output, fx contains the value of the function, Dfx its gradient and D2fx its Hessian matrix. This function is optimized and performs much better than calling pnl_basis_eval, pnl_basis_eval_D and pnl_basis_eval_D2 sequentially.
double pnl_basis_eval_vect (const PnlBasis *basis, const PnlVect *coef, const PnlVect *x)
Description Compute the linear combination of P_k(x) defined by coef. Given the coefficients computed by the function pnl_basis_fit_ls, this function returns ∑ _k=0ⁿcoef_kP_k(x).
double pnl_basis_eval_D_vect (const PnlBasis *basis, const PnlVect *coef, const PnlVect *x, int i)
Description Compute the derivative with respect to x_i of the linear combination of P_k(x) defined by coef. Given the coefficients computed by the function pnl_basis_fit_ls, this function returns ∂_{x_i} ∑ _k=0ⁿcoef_kP_k(x) The index i may vary between 0 and P->nb_variates - 1.
double pnl_basis_eval_D2_vect (const PnlBasis *basis, const PnlVect *coef, const PnlVect *x, int i, int j)
Description Compute the derivative with respect to x_i of the linear combination of P_k(x) defined by coef. Given the coefficients computed by the function pnl_basis_fit_ls, this function returns ∂_{x_i}∂_{x_j} ∑ _k=0ⁿcoef_kP_k(x). The indices i and j may vary between 0 and P->nb_variates - 1.

The following functions are provided for compatibility purposes but are marked as deprecated. Use the functions with the _vect extension.

double pnl_basis_ik (const PnlBasis *b, const double *x, int i, int k)
Description Same as function pnl_basis_ik_vect but takes a C array as the point of evaluation.
double pnl_basis_i (PnlBasis *b, double *x, int i)
Description Same as function pnl_basis_i_vect but takes a C array as the point of evaluation.
double pnl_basis_i_D ( const PnlBasis *b, const double *x, int i, int j )
Description Same as function pnl_basis_i_D_vect but takes a C array as the point of evaluation.
double pnl_basis_i_D2 (const PnlBasis *b, const double *x, int i, int j1, int j2)
Description Same as function pnl_basis_i_D2_vect but takes a C array as the point of evaluation.
double pnl_basis_eval (PnlBasis *P, PnlVect *coef, double *x)
Description Same as function pnl_basis_eval_vect but takes a C array as the point of evaluation.
double pnl_basis_eval_D (PnlBasis *P, PnlVect *coef, double *x, int i)
Description Same as function pnl_basis_eval_D_vect but takes a C array as the point of evaluation.
double pnl_basis_eval_D2 (PnlBasis *P, PnlVect *coef, double *x, int i, int j)
Description Same as function pnl_basis_eval_D2_vect but takes a C array as the point of evaluation.
void pnl_basis_eval_derivs (PnlBasis *P, PnlVect *coef, double *x, double *fx, PnlVect *Dfx, PnlMat *D2fx)
Description Same as function pnl_basis_eval_derivs_vect but takes a C array as the point of evaluation.

[next] [prev] [prev-tail] [front] [up]