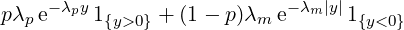6 Random Number Generators
The functionalities described in this chapter are declared in pnl/pnl_random.h.
Random number generators should be called through the new rng interface based on the
PnlRng object. This interface uses reentrant functions and is suitable for multi-threaded
applications.
The older rand interface is kept for compatibility purposes only and should not be used in new code.
| Random generator | index | Type | Info |
|
|
|
|
| KNUTH | PNL_RNG_KNUTH | pseudo | |
| MRGK3 | PNL_RNG_MRGK3 | pseudo | |
| MRGK5 | PNL_RNG_MRGK5 | pseudo | |
| SHUFL | PNL_RNG_SHUFL | pseudo | |
| L’ECUYER | PNL_RNG_L_ECUYER | pseudo | |
| TAUSWORTHE | PNL_RNG_TAUSWORTHE | pseudo | |
| MERSENNE | PNL_RNG_MERSENNE | pseudo | |
| SQRT | PNL_RNG_SQRT | quasi | |
| HALTON | PNL_RNG_HALTON | quasi | |
| FAURE | PNL_RNG_FAURE | quasi | |
| SOBOL_I4 | PNL_RNG_SOBOL_I4 | quasi | uses 32 bit intergers |
| SOBOL_I8 | PNL_RNG_SOBOL2_I8 | quasi | uses 64 bit intergers |
| NIEDERREITER | PNL_RNG_NIEDERREITER | quasi | |
Table 2: Indices of the random generators
6.1 The rng interface
It is possible to create several random number generators each with its own state variable so that
they can evolve independently in a shared memory environment. These generators are suitable for
use in multi-threaded programs.
typedef struct _PnlRng PnlRng;
struct _PnlRng
{
PnlObject object;
int type; /*!< generator type *
void (*Compute)(PnlRng *g, double *sample); /*!< the function to compute the
next number in the sequence */
int rand_or_quasi; /*!< can be PNL_MC or PNL_QMC */
int dimension; /*!< dimension of the space in which we draw the samples */
int counter; /*!< counter = number of samples already drawn */
int has_gauss; /*!< Is a gaussian deviate available? */
double gauss; /*!< If has_gauss==1, gauss a gaussian sample */
int size_state; /*!< size in bytes of the state variable */
void *state; /*!< state of the random generator */
};
-
void pnl_rng_free (PnlRng **)
Description Free a PnlRng .
-
PnlRng * pnl_rng_create (int type)
Description Create a PnlRng corresponding to type which can be any of the values
PNL_RNG_XXX listed in Table 2 which correspond to pseudo random number
generators. Once a generator has been created, you must call pnl_rng_sseed before
using it.
-
void pnl_rng_sseed (PnlRng *rng, unsigned long int s)
Description Set the seed of the genrator rng using s. If s=0, then a default seed
(depending on the generator) is used.
-
int pnl_rng_sdim (PnlRng *rng, int dim)
Description Set the dimension of the state space for a QMC generator and initializes
it accordingly. Returns OK if the generator has been initialized properly and FAIL
otherwise.
-
PnlRng * pnl_rng_copy (const PnlRng *rng)
Description Create a copy of rng.
-
void pnl_rng_clone (PnlRng *dest, const PnlRng *src)
Description Copy the content of src into the already existing basis dest. On exit, src
and dest are identical but independent.
-
PnlRng * pnl_rng_dcmt_create_id (int id, ulong seed)
Description Create a generator with type PNL_RNG_DCMT and identifier id. Two
generators with different ids are independent. Note that the returned generator must
be initialized with pnl_rng_sseed before usage. The identifier id can for instance
correspond to the thread number or the processor rank in parallel computing.
-
PnlRng ** pnl_rng_dcmt_create_array_id (int start_id, int max_id, ulong
seed, int *count)
Description Create an array of generators with types PNL_RNG_DCMT and
identifiers linearly varying between start_id and max_id. The number of generators
created is max_id - start_id + 1. All the generators are independent. Note that each
generator of the returned array must be initialized with pnl_rng_sseed before usage.
-
PnlRng ** pnl_rng_dcmt_create_array (int n, ulong seed, int *count)
Description Create an array of n independent DCMT. seed is the seed used to
initialize the Mersenne Twister generator internally used to find new DCMT. On exit,
count contains the number of generators actually created. Before using the generators,
you must initialize each of them by calling the function pnl_rng_sseed count times.
Some auxiliary functions internally used (to be used with caution)
-
PnlRng * pnl_rng_new ()
Description Create an empty PnlRng .
-
void pnl_rng_init (PnlRng *rng, int type)
Description Initialize an empty PnlRng as returned by pnl_rng_new to become
a generator of type type which can be any of the values PNL_RNG_XXX
listed in Table 2 which correspond to pseudo random number generators. Calling
pnl_rng_create is equivalent to calling first pnl_rng_new and then pnl_rng_init.
-
PnlRng * pnl_rng_get_from_id (int id)
Description Return the global generator described by its macro name. The variable
id can be any of the values PNL_RNG_XXX listed in Table 2.
The following functions return one sample from the specified distribution.
-
int pnl_rng_bernoulli (double p, PnlRng *rng)
Description Generate a sample from the Bernouilli law on {0,1} with parameter p.
-
long pnl_rng_poisson (double lambda, PnlRng *rng)
Description Generate a sample from the Poisson law with parameter lambda.
-
double pnl_rng_exp (double lambda, PnlRng *rng)
Description Generate a sample from the Exponential law with parameter lambda.
-
double pnl_rng_dblexp (double lambda_p, double lambda_m, double p, PnlRng
*rng)
Description Generate a sample from the asymmetric exponential distribution with
density
where λp > 0,λm > 0 and p ∈ [0,1].
-
double pnl_rng_uni (PnlRng *rng)
Description Generate a sample from the Uniform law on ]0,1].
-
double pnl_rng_uni_ab (double a, double b, PnlRng *rng)
Description Generate a sample from the Uniform law on [a,b].
-
double pnl_rng_normal (PnlRng *rng)
Description Generate a sample from the standard normal distribution.
-
double pnl_rng_lognormal (double m, double sigma2, PnlRng *rng)
Description Generate a sample from the log-normal distribution. The underlying normal
distribution has mean m and variance sigma2.
-
double pnl_rng_invgauss (double mu, double lambda, PnlRng *rng)
Description Generate a sample from the inverse Gaussian distribution with mean mu and
shape parameter lambda.
-
long pnl_rng_poisson1 (double lambda, double t,PnlRng *rng)
Description Generate a sample from a Poisson process with intensity lambda at time
t.
-
double pnl_rng_gamma (double a, double b, PnlRng *rng)
Description Generate a sample from the Γ(a,b) distribution.
-
double pnl_rng_chi2 (double df, PnlRng *rng)
Description Generate a sample from the centered χ2(df) distribution.
-
double pnl_rng_ncchi2 (double df, double xnonc, PnlRng *rng)
Description Generate a sample from the non central χ2 distribution with df degrees of
freedom and non central parameter xnonc.
-
double pnl_rng_bessel (double v, double a,PnlRng *rng)
Description Generate a sample from the Bessel distribution with parameters v > -1 and a
> 0.
-
double pnl_rng_gauss (int d, int create_or_retrieve, int index, PnlRng *rng)
Description The second argument can be either CREATE (to actually draw the sample) or
RETRIEVE (to retrieve that element of index index). With CREATE, it draws d random
normal variables and stores them for future usage. They can be withdrawn using RETRIEVE
with the index of the number to be retrieved.
The following functions take an already existing PnlVect *as first argument and fill each entry of
the vector with a sample from the specified distribution. All the entries are independent. The
difference between n-samples from a distribution in dimension 1, and one sample from the same
distribution in dimension n only matters when using a quasi random number generator.
-
void pnl_vect_rng_bernoulli (PnlVect *V, int samples, double a, double b, double
p, PnlRng *rng)
Description Simulate an i.i.d. sample from the Bernoulli distribution with values in
a,b and parameter p. The result is stored in V.
-
void pnl_vect_rng_bernoulli_d (PnlVect *V, int dimension, const PnlVect *a,
const PnlVect *b, const PnlVect *p, PnlRng *rng)
Description Simulate a random vector according to the Bernoulli distribution with
values in {a,b} and parameter p. The result is stored in V, ie. V(i) follows a Bernoulli
distribution on {a(i), b(i)} with parameter p(i).
-
void pnl_vect_rng_poisson (PnlVect *V, int samples, double lambda, PnlRng
*rng)
Description Simulate an i.i.d. sample from the Poisson distribution with parameter
lambda. The result is stored in V. Note that, we are using double based vectors and not
integer based vectors.
-
void pnl_vect_rng_poisson_d (PnlVect *V, int dimension, const PnlVect
*lambda, PnlRng *rng)
Description Simulate a random vector according to the Poisson distribution with
vector parameter lambda. The result is stored in V, ie. V(i) follows a Poisson
distribution with parameter lambda(i). Note that, we are using double based vectors
and not integer based vectors.
-
void pnl_vect_rng_uni (PnlVect *G, int samples, double a, double b, PnlRng
*rng)
Description G is a vector of independent and identically distributed samples from
the uniform distribution on [a,b].
-
void pnl_vect_rng_normal (PnlVect *G, int samples, PnlRng *rng)
Description G is a vector of independent and identically distributed samples from
the standard normal distribution.
-
void pnl_vect_rng_uni_d (PnlVect *G, int d, double a, double b, PnlRng *rng)
Description G is a sample from the uniform distribution on [a,b]d.
-
void pnl_vect_rng_normal_d (PnlVect *G, int d, PnlRng *rng)
Description G is a sample from the d-dimensional standard normal distribution.
The following functions take an already existing PnlMat *as first argument and fill each entry of the
matrix with a sample from the specified distribution. All the entries are independent. On
return, the matrix M is of size samples x dimension. The rows of M are independent and
identically distributed. Each row is a sample from the given law in dimension dimension.
-
void pnl_mat_rng_uni (PnlMat *M, int samples, int d, const PnlVect *a, const
PnlVect *b, PnlRng *rng)
Description M contains samples samples from the uniform distribution on
∏
i=1d[ai,bi].
-
void pnl_mat_rng_uni2 (PnlMat *M, int samples, int d, double a, double b,
PnlRng *rng)
Description M contains samples samples from the uniform distribution on [a,b]d.
-
void pnl_mat_rng_normal (PnlMat *M, int samples, int d, PnlRng *rng)
Description M contains samples samples from the d-dimensional standard normal
distribution.
-
void pnl_mat_rng_bernoulli (PnlMat *M, int samples, int dimension, const
PnlVect *a, const PnlVect *b, const PnlVect *p, PnlRng *rng)
Description Compute a random matrix with independent rows, each of them having
a vector Bernoulli distribution, ie. M(i, j) follows a Bernoulli distribution on {a(j), b(j)}
with parameter p(j).
-
void pnl_mat_rng_poisson (PnlMat *M, int samples, int dimension, const
PnlVect *lambda, PnlRng *rng)
Description Compute a random matrix with independent rows, each of them having
a vector Poisson distribution, ie. M(i, j) follows a Poisson distribution with parameter
p(j).
Some examples
#include <stdlib.h>
#include "pnl/pnl_random.h"
int main ()
{
int i, M;
PnlRng *rng = pnl_rng_create(PNL_RNG_MERSENNE);
PnlVect *v = pnl_vect_new();
M = 10000;
/* rng must be initialized. When sseed=0, a default
value depending on the generator is used */
pnl_rng_sseed(rng, 0);
for (i=0 ; i<M ; i++)
{
/* Simulates a normal random vector in R^{10} */
pnl_vect_rng_normal(v, 10, rng);
/* Do something with v */
}
pnl_vect_free(&v);
pnl_rng_free(&rng); /* Frees the generator */
exit(0);
}
#include <stdlib.h>
#include <time.h>
#include "pnl/pnl_random.h"
int main ()
{
int i, M;
double E;
PnlRng *rng = pnl_rng_create(PNL_RNG_MERSENNE);
M = 10000;
/* rng must be initialized. */
pnl_rng_sseed(rng, time (NULL));
for (i=0 ; i<M ; i++)
{
/* Simulates an exponential random variable */
E = pnl_rng_exp(1, rng);
/* Do something with E */
}
pnl_rng_free(&rng); /* Frees the generator */
exit(0);
}
6.2 The rand interface (deprecated)
Note: For backward compatibility with older versions of the PNL, we still provide the old rand
interface to random number generation although we strongly encourage users to use the new rng
interface (see section 6.1).
Every generator is identified by an integer valued macro. One must NOT refer to a generator using
directly the value of the macro PNL_RNG_XXX because there is no warranty that the order used
to store the generators will remain the same in future releases. Instead, one should call generators
directly using their macro names.
The initial seeds of all the generators are fixed by the function pnl_rand_init but you can change it
by calling pnl_rand_sseed.
Before starting to use random number generators, you must initialize them by calling
-
int pnl_rand_init (int type_generator, int simulation_dim, long samples)
Description It resets the sample counter to 0 and checks that the generator described
by type_generator can actually generate samples in dimension simulation_dim and
fixes the seed.
-
int pnl_rand_or_quasi (int type_generator)
Description Return the type the generator of index type_generator, PNL_MC or
PNL_QMC
-
void pnl_rand_sseed ((int type_generator, unsigned long int seed))
Description It sets the seed of the generator type_generator with seed.
-
const char * pnl_rand_name (int type_generator)
Description Return the name of the generator of index type_generator
Once a generator is chosen, there are several functions available in the library to draw samples
according to a given law.
The following functions return one sample from a specified law.
-
int pnl_rand_bernoulli (double p, int type_generator)
Description Generate a sample from the Bernouilli law on {0,1} with parameter p.
-
long pnl_rand_poisson (double lambda, int type_generator)
Description Generate a sample from the Poisson law with parameter lambda.
-
double pnl_rand_exp (double lambda, int type_generator)
Description Generate a sample from the Exponential law with parameter lambda.
-
double pnl_rand_uni (int type_generator)
Description Generate a sample from the Uniform law on [0,1].
-
double pnl_rand_uni_ab (double a, double b, int type_generator)
Description Generate a sample from the Uniform law on [a,b].
-
double pnl_rand_normal (int type_generator)
Description Generate a sample from the standard normal distribution.
-
long pnl_rand_poisson1 (double lambda, double t, int type_generator)
Description Generate a sample from a Poisson process with intensity lambda at time
t.
-
double pnl_rand_gamma (double a, double b, int type_generator)
Description Generate a sample from the Γ(a,b) distribution.
-
double pnl_rand_chi2 (double n, int type_generator)
Description Generate a sample from the centered χ2(n) distribution.
-
double pnl_rand_bessel (double v, double a, int generator)
Description Generate a sample from the Bessel distribution with parameters v > -1
and a > 0.
The following functions take an already existing PnlVect * as its first argument and fill each entry
of the vector with a sample from the specified law. All the entries are independent. The difference
between n-samples from a distribution in dimension 1, and one sample from the same
distribution in dimension n only matters when using a Quasi random number generator.
-
void pnl_vect_rand_uni (PnlVect *G, int samples, double a, double b, int
type_generator)
Description G is a vector of independent and identically distributed samples from
the uniform distribution on [a,b].
-
void pnl_vect_rand_normal (PnlVect *G, int samples, int generator)
Description G is a vector of independent and identically distributed samples from
the standard normal distribution.
-
void pnl_vect_rand_uni_d (PnlVect *G, int d, double a, double b, int
type_generator)
Description G is a sample from the uniform distribution on [a,b]d.
-
void pnl_vect_rand_normal_d (PnlVect *G, int d, int generator)
Description G is a sample from the d-dimensional standard normal distribution.
The following functions take an already existing PnlMat * as first argument and fill each entry of
the vector with a sample from the specified law. All the entries are in-dependant. On return,
the matrix M is of size samples x dimension. The rows of M are independently and
identically distributed. Each row is a sample from the given law in dimension dimension.
-
void pnl_mat_rand_uni (PnlMat *M, int samples, int d, const PnlVect *a, const
PnlVect *b, int type_generator)
Description M contains samples samples from the uniform distribution on
∏
i=1d[ai,bi].
-
void pnl_mat_rand_uni2 (PnlMat *M, int samples, int d, double a, double b, int
type_generator)
Description M contains samples samples from the uniform distribution on [a,b]d.
-
void pnl_mat_rand_normal (PnlMat *M, int samples, int d, int type_generator)
Description M contains samples samples from the d-dimensional standard normal
distribution.
Because of the use of Quasi random number generators, you may need to draw a set of samples at
once because they represent one sample from a multi-dimensional distribution. The following
function enables to draw one sample from the dimension-dimensional standard normal
distribution and store it so that you can access the elements individually afterwards.
-
double pnl_rand_gauss (int d, int create_or_retrieve, int index, int
type_generator)
Description The second argument can be either CREATE (to actually draw the
sample) or RETRIEVE (to retrieve that element of index index). With CREATE,
it draws d random normal variables and stores them for future usage. They can be
withdrawn using RETRIEVE with the index of the number to be retrieved.