The macros and functions of this paragraph are defined in pnl/pnl_mathtools.h.
A few mathematical constants are provided by the library. Most of them are actually already defined in math.h, values.h or limits.h and a few others have been added.
PNL_IS_ODD (int n)
Description Return 1 if n is odd and 0 otherwise.
PNL_IS_EVEN (int n)
Description Return 1 if n is even and 0 otherwise.
PNL_SIGN (x)
Description Return the sign of x (-1 if x < 0, 0 otheriwse).
int pnl_isinf (double x)
Description Return +1 if x=+Inf, -1 if x=-Inf and 0 otherwise.
int pnl_isfinite (double x)
Description Return 1 if x!=+-Inf
int pnl_itrunc (double s)
Description This function is similar to the trunc function (provided by the C library)
but the result is typed as an integer instead of a double. Digits may be lost if s exceeds
MAX_INT.
long int pnl_ltrunc (double s)
Description This function is similar to the trunc function (provided by the C library)
but the result is typed as a long integer instead of a double.
double pnl_trunc (double s)
Description Return the nearest integer not greater than the absolute value of s. This
function is part of C99 as trunc.
double pnl_round (double s)
Description Return the integral value nearest to x rounding half-way cases away from
zero, regardless of the current rounding direction. This function is part of C99 as round.
int pnl_iround (double s)
Description This function is similar to the round function (provided by the C library)
but the result is typed as an integer instead of a double. Digits may be lost if s exceeds
MAX_INT.
long int pnl_lround (double s)
Description This function is similar to the round function (provided by the C library)
but the result is typed as a long integer instead of a double.
double pnl_fact (double x)
Description See pnl_sf_fact
double pnl_lgamma (double x)
Description See pnl_sf_log_gamma
double pnl_tgamma (double x)
Description See pnl_sf_gamma
double pnl_log1p (double x)
Description Compute log(1+x) accurately for small values of x
double pnl_expm1 (double x)
Description Compute exp(x)-1 accurately for small values of x
double pnl_cosm1 (double x)
Description Compute cos(x)-1 accurately for small values of x
double pnl_pow_i (double x, int n)
Description Compute x^n for an integer n.
int pnl_isequal_rel (double x, double y, double relerr)
Description Compare two floating–point numbers up to a relative precision relerr
int pnl_isequal_abs (double x, double y, double abserr)
Description Compare two floating–point numbers up to an absolute precision abserr
int pnl_isequal (double x, double y, double relerr)
Description Equivalent to pnl_isequal_abs if |x| < 1 and to pnl_isequal_abs
otherwise.
The complex type and related functions are defined in the header pnl/pnl_complex.h.
The first native implementation of complex numbers in the C language appeared in C99, which is unfortunately not available on all platforms. For this reason, we provide here an implementation of complex numbers.
typedef struct { double r; /*!< real part */ double i; /*!< imaginary part */ } dcomplex;
dcomplex Complex_polar (double r, double theta)
Description r exp(i theta)
double Creal (dcomplex z)
Description R(z)
double Cimag (dcomplex z)
Description Im(z)
dcomplex CRadd (dcomplex z, double b)
Description z+b
dcomplex RCadd (double b, dcomplex z)
Description b+z
dcomplex CRsub (dcomplex z, double b)
Description z-b
dcomplex RCsub (double b, dcomplex z)
Description b-z
dcomplex Cminus (dcomplex z)
Description -z
dcomplex RCmul (double x, dcomplex z)
Description x*z
dcomplex CRmul (dcomplex z, double x)
Description z * x
dcomplex CRdiv (dcomplex z, double x)
Description z/x
dcomplex RCdiv (double x, dcomplex z)
Description x/z
dcomplex Conj (dcomplex z)
Description z
dcomplex Cinv (dcomplex z)
Description 1/z
double Csqr_norm (dcomplex z)
Description Re(z)2 + im(z)2
double Cabs (dcomplex z)
Description |z|
dcomplex Csqrt (dcomplex z)
Description sqrt(z) , square root (with positive real part)
dcomplex Clog (dcomplex z)
Description log(z)
dcomplex Cexp (dcomplex z)
Description exp(z)
dcomplex Cpow (dcomplex z, dcomplex w)
Description zw, power function
dcomplex Cpow_real (dcomplex z, double x)
Description zx, power function
dcomplex Ccos (dcomplex z)
Description cos(g)
dcomplex Csin (dcomplex z)
Description sin(g)
dcomplex Ctan (dcomplex z)
Description tan(z)
dcomplex Ccotan (dcomplex z)
Description cotan(z)
dcomplex Ccosh (dcomplex z)
Description cosh(g)
dcomplex Csinh (dcomplex z)
Description sinh(g)
dcomplex Ctanh (dcomplex z)
Description tanh(z) = 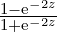
dcomplex Ccotanh (dcomplex z)
Description cotanh(z) = 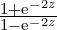
double Carg (dcomplex z)
Description arg(z)
dcomplex Ctgamma (dcomplex z)
Description Gamma(z), the Gamma function
dcomplex Clgamma (dcomplex z)
Description log(Gamma (z)), the logarithm of the Gamma function
void Cprintf (dcomplex z)
Description Print a complex number on the standard output
int pnl_complex_isequal_abs (dcomplex x, dcomplex y, double abserr)
Description Test if two complex numbers are equal up to an absolute error abserr.
int pnl_complex_isequal_rel (dcomplex x, dcomplex y, double relerr)
Description Test if two complex numbers are equal up to a relative error relerr.
int pnl_complex_isequal (dcomplex x, dcomplex y, double err)
Description Test if two complex numbers using one of the above functions depending
on the magnitude of |y|.
Most algebraic operations on complex numbers are implemented using the following naming for the functions
All these function names begin in C_op_,
The small letters a, b denote two complex numbers whereas d is a real number,
The letter i denotes the multiplication by the pure imagniary number 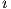 ,
,
The letter c indicates that the next coming number is conjugated.
The letters p, m denote the two standard operations plus and minus respectively.
For example C_op_idamcb is 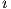 d
d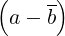 . So functions are :
. So functions are :
dcomplex C_op_apib (dcomplex a, dcomplex b)
Description a + 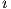 b.
b.
dcomplex C_op_apcb (dcomplex a, dcomplex b)
Description a + b.
dcomplex C_op_amcb (dcomplex a, dcomplex b)
Description a -b.
dcomplex C_op_amib (dcomplex a, dcomplex b)
Description a - i b
dcomplex C_op_dapb (double d, dcomplex a, dcomplex b)
Description d(a + b).
dcomplex C_op_damb (double d, dcomplex a, dcomplex b)
Description d(a -b).
dcomplex C_op_dapib (double d, dcomplex a, dcomplex b)
Description d(a + 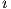 b).
b).
dcomplex C_op_damib (double d, dcomplex a, dcomplex b)
Description d(a -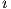 b).
b).
dcomplex C_op_dapcb (double d, dcomplex a, dcomplex b)
Description d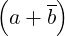 .
.
dcomplex C_op_damcb (double d, dcomplex a, dcomplex b)
Description d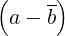 .
.
dcomplex C_op_idapb (double d, dcomplex a, dcomplex b)
Description 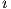 d
d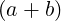 .
.
dcomplex C_op_idamb (double d, dcomplex a, dcomplex b)
Description 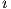 d
d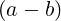 .
.
dcomplex C_op_idapcb (double d, dcomplex a, dcomplex b)
Description 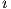 d
d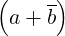 .
.
dcomplex C_op_idamcb (double d, dcomplex a, dcomplex b)
Description 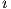 d
d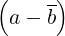 .
.